Understanding time and space complexity is important when choosing between different algorithms. Time complexity is the amount of time an algorithm takes based on the length of the input. Space complexity is how much memory an algorithm requires based on the size of the input. Technically, there are worst case, average case, and best case scenarios for analyzing algorithms, but we typically consider the worst case scenarios. For worst case scenarios, we calculate the upper bound on the running time of an algorithm or the memory requirements. Big-O notation only considers the dominant term in the running time equation.

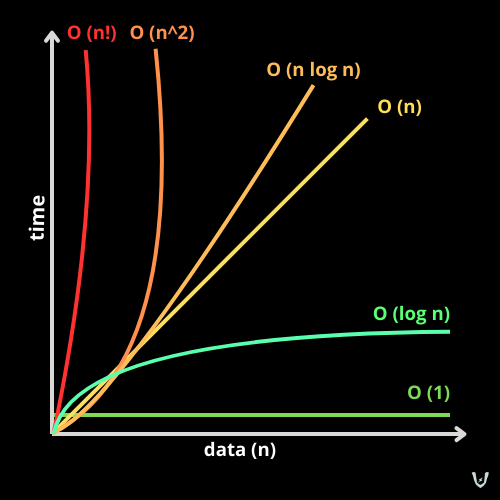
Big O Notation Graph by LFebro

Thanks for reading Learning Data Structures and Algorithms with Music! Subscribe for free to receive new posts and support my work.

The most common complexities are O(1), O(logn), O(n), O(nlogn), O(n^2), O(2^n), and O(n!).

O(1)

O(1) has constant time complexity in which the execution time is the same regardless of the size of the input. Look-ups in dictionaries, accessing arrays, and pushing and popping elements from a stack are all O(1).

This code is O(1) because it is a constant number of operations. It doesn’t change or grow based on the input (which makes it constant). It is the best complexity possible and is for very large n (>10^9).

a = [50, 50, 50, 50, 50] melody = music21.converter.parseFile('O1.mid') melody.show('midi')

O(logn)

The log(n) function (log base 2 of n) grows very slowly. Log(1000000) is about 20 and Log(2000000) is about 21. You will see log(n) complexity for algorithms that halve n for each iteration, such as with binary search. It is still for very large n (>10^8).

import math

N = 200
result = [N]
while N > 1:
  # some constant operation
    N = N/2
    print(N)
    result.append(N)

result_ceil = [math.ceil(x) for x in result] 
print(result_ceil)

[200, 100, 50, 25, 13, 7, 4, 2, 1]

melody = music21.converter.parseFile('Ologn.mid')
melody.show('midi')

The audio is long because the MIDI is not audible in the very low numbers.

O(n)

O(n) is linear time. It means increasing linearly with the size of the input data. Some examples are going through an array or a list one element at a time, stacks and queues, and two pointers. This is typically used for n < 10^6.

# O(n)

N = 50
i = 20
MIDI_list = []
while i < N:
  # constant time code
  MIDI_list.append(i)
  i += 1

print(MIDI_list)

melody = music21.converter.parseFile('On.mid')
melody.show('midi')

O(nlogn)

O(nlogn) is like doing binary search n times, hence the n log(n). For questions that want the “top n elements”, you can push or pop to heap to n times. It’s useful for sorting, as the default sorting algorithm’s expected runtime is nlog(n). Divide and conquer and quick sort are some examples. This is typically used for n < 10^6 as well.

array_num = [10,50,20,25,100,60,75,80,90]

melody = music21.converter.parseFile('Onlogn_unsorted.mid')
melody.show('midi')

array_num.sort() # sorts in place

melody = music21.converter.parseFile('Onlogn.mid')
melody.show('midi')

Thanks for reading Learning Data Structures and Algorithms with Music! Subscribe for free to receive new posts and support my work.

O(n^2)

O(n^2) is also called quadratic time. Time is proportional to the square of the number of elements. Nested loops and many brute force solutions are quadratic time. This is typically used for n < 3000. Bubble sort is quadratic time.

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j] # if the next element is greater than the previous one, swap it.

    return(arr)

arr = [64, 34, 50, 12, 70, 11, 90]
melody = music21.converter.parseFile('Onsqrt_unsorted.mid')
melody.show('midi')

 arr_sort = bubble_sort(arr)
print(arr_sort)

[11, 12, 34, 50, 64, 70, 90]

melody = music21.converter.parseFile('Onsqrt_unsorted.mid')
melody.show('midi')

O(2^n)

Also called exponential time, these problems grow very rapidly. These problems often require memoization to avoid repeated computations and reduce complexity. They apply for combinatorial problems and often use recursion. The Fibonacci algorithm example of a recursive algorithm that is O(2^n) because we call two recursive calls, Fib(i-1) and Fib(i-2), for each Fib(i) where i > 1. The time complexity of this algorithm is determined by the number of recursive calls. Each recursive call processes one element. The running time of each recursive call is O(1) , so the total running time is O(2^n). They are best done with n < 20.

def Fib(n):
  if n == 0 or n == 1:
    return 1
  return Fib(n - 1) + Fib(n - 2)

n = 11

melody = music21.converter.parseFile('O2n_unsorted.mid')
melody.show('midi')

answer = Fib(n)


print(answer)

144

melody = music21.converter.parseFile('O2n.mid')
melody.show('midi')

O(n!)

Finally, we have factorial time, O(n!). It grows extremely big, so it can only work for small sizes, n <= 12. Similar to exponetial time algorithms, it often requires memoization to avoid repeated computations and reduce complexity. Problems that have this complexity are combinatorial problems, such as permutations. They often involve recursion as well. Below is example is an algorithm that lists all permutations of the factorial.

def factorial(n):
    for each in range(n):
        print(n)
        factorial(n-1)

factorial(n)

melody = music21.converter.parseFile('Ofact.mid')
melody.show('midi')

For all of these algorithms, space complexity works similarly, but we are considering memory as the unit instead of the data as the unit.

Here is the link to the Jupyter Notebook to play it in your browser. Enjoy!

Thanks for reading Learning Data Structures and Algorithms with Music! Subscribe for free to receive new posts and support my work.